top of page
中学理科の自習学習
④ 凸レンズのはたらき
教科書P.190

図のような ガラス (プリズム) に
左の方から 光を当てると

プリズムを通りぬける光は

まず プリズムに入るときに
青色の矢印のように屈折します

さらに 光がプリズムから出るときにも
黄緑色の矢印のように屈折します
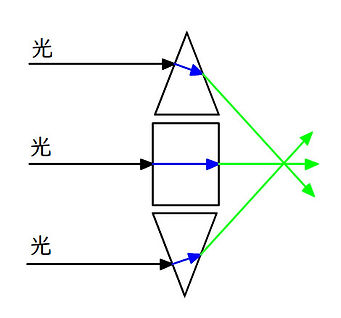



図のように
3つのプリズムに 平行な光��を当てると
屈折した光が 1点に集まります
曲面を使って 平行な光をすべて
1点に集まるようにしたのが
凸レンズ です
凸レンズ では
光が 入るときと 出るときの2回の屈折を
きちんと書くと かえってわかりにくくなるので
図のように レンズの中央で1度だけ屈折した
ように 省略した書き方をします
凸レンズに入る平行な光は1点に集まります
平行に入った光が集まる点Fを
といいます
凸レンズの中心Oから Fまでの距離を
といいます
この距離は 凸レンズによって違います
【 凸レンズによってできる像 】
屈折後の光の進み方
凸レンズを通過するたくさんの光のうち
図のA~Cの3つの光は特徴的な進み方をします

光軸
Aは 凸レンズの中心に進む光
Bは 光軸と平行に進む光
Cは 凸レンズの手前の焦点Fを通る光

Aは そのまま真っ直ぐ進みます
Bは 屈折した後 向こうの焦点Fを通ります
Cは 屈折した後 光軸と平行に進みます
AとBの光の進み方を考えることが
凸レンズの問題を解くときの基本となります

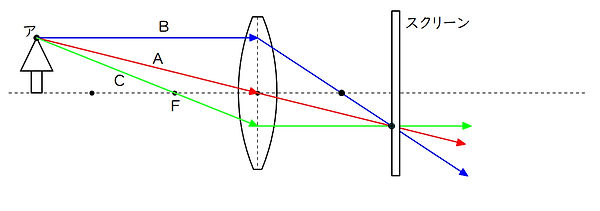
上図の位置にスクリーンを置くと
物体のアから出た光が
Aのように進むと スクリーンのaに当たり
Bのよう�に進むと スクリーンのbに当たり
Cのように進むと スクリーンのcに当たります
点アからの光が a,b,cに分散するので
スクリーンにはぼやけた像ができてしまいます
上図の位置にスクリーンを置くと
物体のアから出た光が すべて1点に集まりますから
スクリーンに きれいな像が映るのです

上図のように スクリーンが後ろにずれても
点アからの光が a,b,cに分散するので
スクリーンにはぼやけた像ができてしまいます

もちろん
点アからの光は、
基本的なA~Cの3つだけではありません
凸レンズは きれいな曲面に作られているので
3つ以�外の光も 屈折後 同じ1点に集まるのです
屈折後の光が集まる位置にスクリーンを置くと
きれいに像が映るのです

上図のパターンで
どの位置にどんな像ができるのか 確かめましょう

物体の上部の点アから出た光は
屈折後 ア’に集まります

物体の下部の点イから出た光は
屈折後 イ’に集まります

ア’とイ’の位置に光が集まるので
その距離にスクリーンを置けば
下図のように
上下左右が逆さまの像が映ります

このような 実際に映る像を
といいます
【 倒立実像のできる位置と大きさ 】
まずは 大事な基本形を

上図のように
凸レンズの焦点距離のち�ょうど2倍の位置に
物体があるときの倒立実像が基本になります
このとき、倒立実像は
焦点距離の2倍の位置にでき
物体と同じ大きさになります
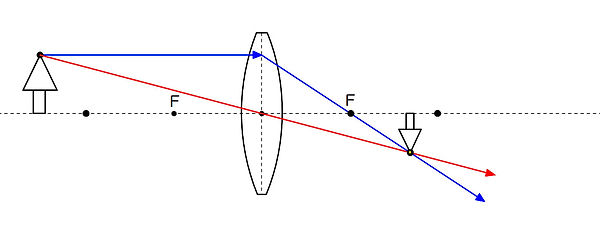
基本形に比べて 物体が遠いとき
(物体が 焦点距離の2倍より遠いとき)
倒立実像は 基本形より
近くに 小さくできます
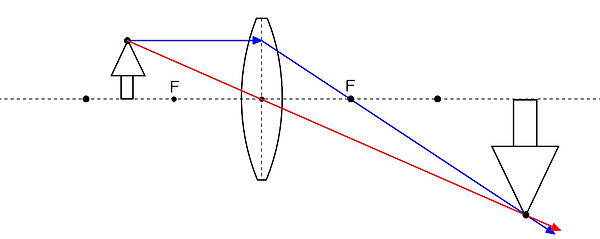
基本形に比べて 物体が近いとき
(物体が 焦点距離の2倍より近いとき)
倒立実像は 基本形より
遠くに 大きくできます
物体が凸レンズに近づくほど
倒立実像は凸レンズから離れて
その分 大きくなりますが……

上図のように
物体が凸レンズの焦点距離にまで近づくと
光が1点に集まらなくなって
倒立実像はできなくなります

物体が焦点距離より近づくと
上図のように
レンズの中心を通りぬける光と
屈折して焦点を通る光が
どんどん離れてしまうのですが

反対側から凸レンズに目を近づけて見ると
点アから出た光が 屈折していることがわからないので
点ア’ から光がやって来ていると錯覚するのです

なので 反対側から見た人には
物体が破線で描いたような大きな物体が見えます
このように 見える像を
といいます
は レンズの中に見えるだけで
実際には存在しません
bottom of page